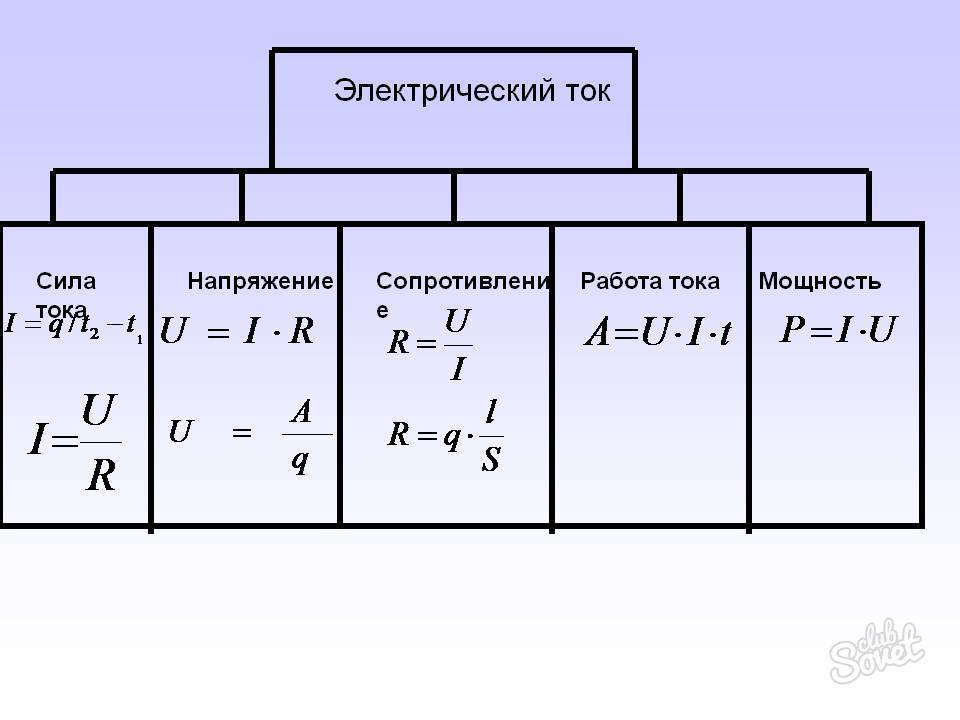
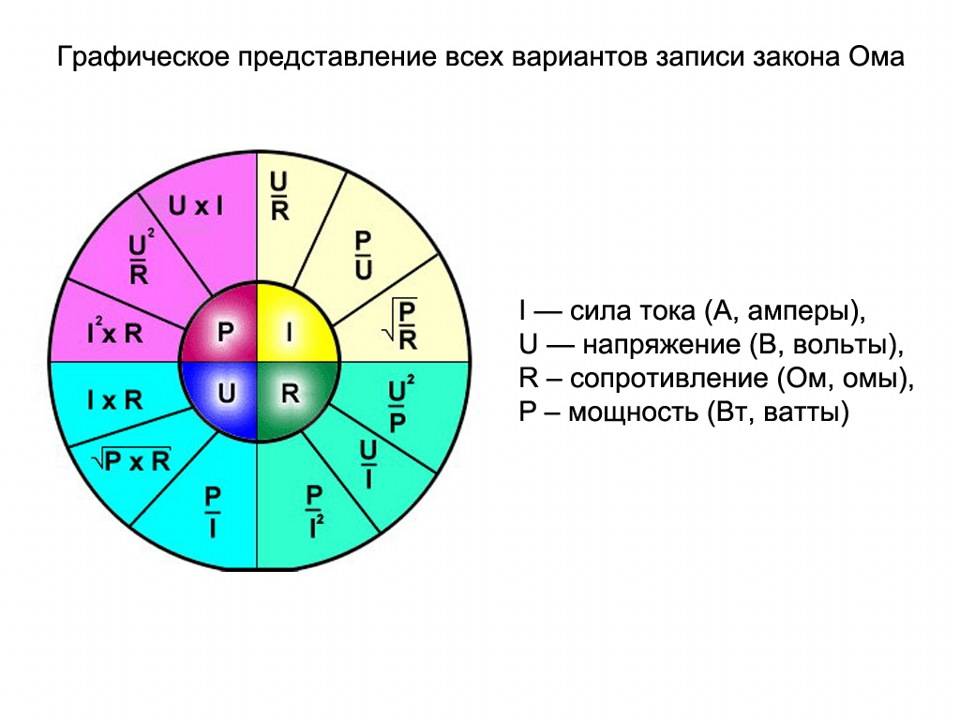
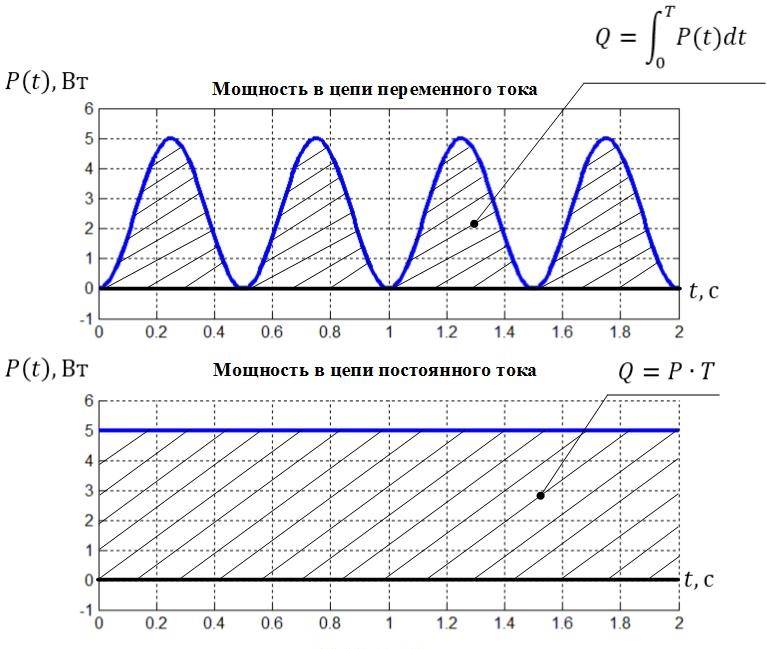
- Càlcul per a connexió en paral·lel i en sèrie
- Càlcul actual
- EXEMPLES DE TASQUES
- Part 1
- Part 2
- Potència total i els seus components
- Càrrega resistiva
- càrrega capacitiva
- Càrrega inductiva
- Circuits elèctrics i les seves varietats
- Característiques
- Per a AC
- 1. Calculadora de dissipació de potència i corrent que flueix en funció de la resistència i la tensió aplicada.
- Càlcul de circuits elèctrics
- Com estalviar diners
- Canvi de resistència:
- Ús de fórmules
- Per a AC
- Preguntes sobre treball i energia elèctrica
- Informació interessant sobre el tema
- Normes d'alimentació de CA
- Mètode de conversió de circuits elèctrics
- Càlcul d'un circuit amb una font d'alimentació
- Càlcul d'un circuit elèctric extens amb múltiples fonts d'alimentació
- Càlcul de corrent per a una xarxa monofàsica
- Conclusió
- Resum de la lliçó
Càlcul per a connexió en paral·lel i en sèrie
Quan es calcula el circuit d'un dispositiu electrònic, sovint cal trobar la potència que s'allibera en un sol element. Aleshores, cal determinar quina tensió hi cau, si estem parlant d'una connexió en sèrie o quin corrent flueix quan es connecta en paral·lel, considerarem casos concrets.
Aquí Itotal és igual a:
I=U/(R1+R2)=12/(10+10)=12/20=0,6
Poder general:
P=UI=12*0,6=7,2 watts
A cada resistència R1 i R2, com que la seva resistència és la mateixa, la tensió cau:
U=IR=0,6*10=6 Volts
I destaca per:
Pen una resistència\u003d IU \u003d 6 * 0,6 \u003d 3,6 watts
Aleshores, amb una connexió paral·lela en aquest esquema:
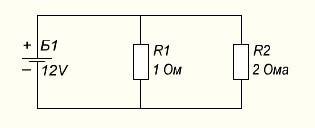
Primer, busquem jo a cada branca:
jo1=U/R1=12/1=12 amperes
jo2=U/R2=12/2=6 amperes
I destaca en cadascun per:
PR1\u003d 12 * 6 \u003d 72 watts
PR2\u003d 12 * 12 \u003d 144 watts
Tots destaquen:
P=UI=12*(6+12)=216 watts
O a través de la resistència total, llavors:
Rgeneral=(R1*R2)/( R1+R2)=(1*2)/(1+2)=2/3=0,66 ohms
I=12/0,66=18 amperes
P=12*18=216 watts
Tots els càlculs coincideixen, de manera que els valors trobats són correctes.
Càlcul actual
La magnitud del corrent es calcula per la potència i és necessària en l'etapa de disseny (planificació) d'un habitatge: un apartament, una casa.
- L'elecció del cable d'alimentació (filferro) a través del qual els dispositius de consum d'energia es poden connectar a la xarxa depèn del valor d'aquest valor.
- Coneixent la tensió de la xarxa elèctrica i la càrrega completa dels aparells elèctrics, és possible, mitjançant la fórmula, calcular la intensitat del corrent que cal fer passar pel conductor (filferro, cable). Segons la seva mida, es selecciona l'àrea de la secció transversal de les venes.
Si es coneixen els consumidors elèctrics de l'apartament o de la casa, cal fer càlculs senzills per muntar correctament el circuit d'alimentació.
Es realitzen càlculs similars amb finalitats de producció: determinar l'àrea de secció transversal necessària dels nuclis del cable quan es connecten equips industrials (diversos motors i mecanismes elèctrics industrials).
EXEMPLES DE TASQUES
Part 1
1. La força del corrent en el conductor es va augmentar 2 vegades. Com canviarà la quantitat de calor alliberada per unitat de temps, sense canviar la resistència del conductor?
1) augmentarà 4 vegades
2) disminuirà 2 vegades
3) augmentarà 2 vegades
4) disminuir 4 vegades
2.La longitud de l'espiral de l'estufa elèctrica es va reduir 2 vegades. Com canviarà la quantitat de calor alliberada a l'espiral per unitat de temps a una tensió de xarxa constant?
1) augmentarà 4 vegades
2) disminuirà 2 vegades
3) augmentarà 2 vegades
4) disminuir 4 vegades
3. La resistència de la resistència \(R_1 \) és quatre vegades menor que la resistència de la resistència \(R_2 \). Treball actual a la resistència 2
1) 4 vegades més que a la resistència 1
2) 16 vegades més que la resistència 1
3) 4 vegades menys que a la resistència 1
4) 16 vegades menys que a la resistència 1
4. La resistència de la resistència \(R_1 \) és 3 vegades la resistència de la resistència \(R_2 \). La quantitat de calor que s'alliberarà a la resistència 1
1) 3 vegades més que a la resistència 2
2) 9 vegades més que la resistència 2
3) 3 vegades menys que a la resistència 2
4) 9 vegades menys que a la resistència 2
5. El circuit es munta a partir d'una font d'alimentació, una bombeta i un fil de ferro prim connectats en sèrie. La bombeta brillarà més si
1) substituïu el cable per un ferro més prim
2) reduir la longitud del cable
3) intercanvieu el cable i la bombeta
4) substituïu el cable de ferro amb nicrom
6. La figura mostra un gràfic de barres. Mostra els valors de voltatge als extrems de dos conductors (1) i (2) de la mateixa resistència. Compareu els valors del treball actual \( A_1 \) i (A_2 \) en aquests conductors durant el mateix temps.
1) \(A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)
7. La figura mostra un gràfic de barres. Mostra els valors de la intensitat del corrent en dos conductors (1) i (2) de la mateixa resistència. Compareu els valors de treball actuals \( A_1 \) i \ ( A_2 \) en aquests conductors durant el mateix temps.
1) \(A_1=A_2 \)
2) \( A_1=3A_2 \)
3) \( 9A_1=A_2 \)
4) \( 3A_1=A_2 \)
8. Si utilitzeu làmpades amb una potència de 60 i 100 W en un canelobre per il·luminar l'habitació, aleshores
A. Hi haurà un gran corrent en una làmpada de 100 W.
B. Una làmpada de 60 W té més resistència.
Veritat(s) és(són) la(s) afirmació(s)
1) només A
2) només B
3) tant A com B
4) ni A ni B
9. Una estufa elèctrica connectada a una font de corrent continu consumeix 108 kJ d'energia en 120 segons. Quina és la força actual de l'espiral de rajoles si la seva resistència és de 25 ohms?
1) 36 A
2) 6 A
3) 2,16 A
4) 1,5 A
10. Una estufa elèctrica amb un corrent de 5 A consumeix 1000 kJ d'energia. Quin és el temps que passa el corrent per l'espiral de la rajola si la seva resistència és de 20 ohms?
1) 10.000 s
2) Anys 2000
3) 10 s
4) 2 s
11. La bobina niquelada de l'estufa elèctrica es va substituir per una bobina de nicrom de la mateixa longitud i àrea de secció transversal. Establir una correspondència entre les magnituds físiques i els seus possibles canvis quan la rajola es connecta a la xarxa elèctrica. Escriu a la taula els números seleccionats sota les lletres corresponents. Els números de la resposta es poden repetir.
QUANTITAT FÍSICA
a) Resistència elèctrica de la bobina
B) La força del corrent elèctric a l'espiral
B) Potència del corrent elèctric consumida per les rajoles
NATURALESA DEL CANVI
1) augmentat
2) disminuït
3) no ha canviat
12. Establir una correspondència entre les magnituds físiques i les fórmules per les quals es determinen aquestes magnituds. Escriu a la taula els números seleccionats sota les lletres corresponents.
QUANTITATS FÍSIQUES
a) Corrent de treball
B) intensitat del corrent
b) Potència actual
FÒRMULA
1) \( \frac{q}{t} \)
2) \(qU \)
3) \( \frac{RS}{L} \)
4) \(UI \)
5) \( \frac{U}{I} \)
Part 2
13.L'escalfador es connecta en sèrie amb un reòstat amb una resistència de 7,5 ohms a una xarxa amb una tensió de 220 V. Quina és la resistència de l'escalfador si la potència del corrent elèctric al reòstat és de 480 W?
Potència total i els seus components
L'energia elèctrica és una quantitat responsable de la velocitat de canvi o transmissió de l'electricitat. La potència aparent es denota amb la lletra S i es troba com el producte dels valors efectius de corrent i tensió. La seva unitat de mesura és volt-ampere (VA; V A).
La potència aparent pot estar formada per dos components: actiu (P) i reactiu (Q).
La potència activa es mesura en watts (W; W), la potència reactiva es mesura en vars (Var).
Depèn de quin tipus de càrrega s'inclou a la cadena de consum d'energia.
Càrrega resistiva
Aquest tipus de càrrega és un element que resisteix el corrent elèctric. Com a resultat, el corrent fa la feina d'escalfar la càrrega i l'electricitat es converteix en calor. Si una resistència de qualsevol resistència es connecta en sèrie amb la bateria, aleshores el corrent que passa pel circuit tancat l'escalfarà fins que la bateria es descarregui.
Atenció! Un exemple d'escalfador elèctric tèrmic (TENA) es pot citar com a càrrega activa en xarxes de CA. La dissipació de calor sobre ell és el resultat del treball de l'electricitat
Aquests consumidors també inclouen bobines de bombetes, estufes elèctriques, forns, planxes, calderes.
càrrega capacitiva
Aquestes càrregues són dispositius que poden acumular energia en camps elèctrics i crear un moviment (oscil·lació) de potència des de la font fins a la càrrega i viceversa.Les càrregues capacitives són condensadors, línies de cable (capacità entre els nuclis), condensadors i inductors connectats en sèrie i paral·lel al circuit. Els amplificadors de potència d'àudio, els motors elèctrics síncrons en mode sobreexcitat també carreguen les línies del component capacitiu.
Càrrega inductiva
Quan el consumidor d'electricitat és un equip determinat, que inclou:
- transformadors;
- motors asíncrons trifàsics, bombes.
A les plaques acoblades a l'equip, es pot veure una característica com el cos ϕ. Aquest és el factor de canvi de fase entre el corrent i la tensió a la xarxa de CA a la qual es connectarà l'equip. També s'anomena factor de potència, com més proper cos ϕ a la unitat, millor.
Important! Quan un dispositiu conté components inductius o capacitius: transformadors, bobines, bobinatges, condensadors, el corrent sinusoïdal retarda la tensió en algun angle de fase. Idealment, la capacitat proporciona un canvi de fase de -900 i la inductància - + 900
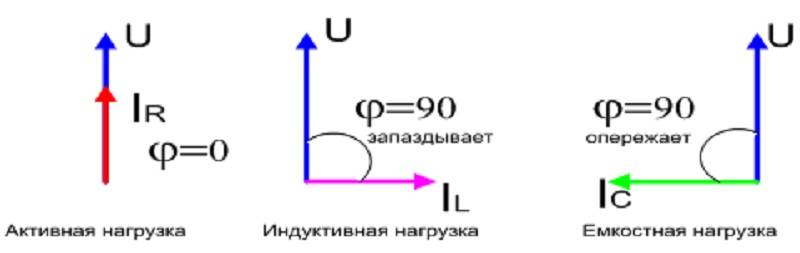 Valors de Cos ϕ en funció del tipus de càrrega
Valors de Cos ϕ en funció del tipus de càrrega
Els components capacitius i inductius formen conjuntament la potència reactiva. Aleshores la fórmula de la potència total és:
S = √ (P2 + Q2),
on:
- S és la potència aparent (VA);
- P és la part activa (W);
- Q és la part reactiva (Var).
Si traceu això gràficament, podeu veure que l'addició vectorial de P i Q serà el valor total de S, la hipotenusa del triangle de potència.
Explicació gràfica de l'essència del poder total
Circuits elèctrics i les seves varietats
Un circuit elèctric és un complex de dispositius i objectes individuals connectats d'una manera determinada. Proporcionen un camí per al pas de l'electricitat.Per caracteritzar la relació entre la càrrega que flueix dins de cada conductor individual durant un temps i la durada d'aquest temps, s'utilitza una determinada magnitud física. I aquest és el corrent al circuit elèctric.
La composició d'aquesta cadena inclou una font d'energia, consumidors d'energia, és a dir. càrrega i cables. Es divideixen en dues varietats:
- No ramificat: el corrent que passa del generador al consumidor d'energia no canvia de valor. Per exemple, això és la il·luminació, que només inclou una bombeta.
- Ramificat: cadenes que tenen algunes branques. El corrent, que es mou des de la font, es divideix i va a la càrrega per diverses branques. Tanmateix, el seu significat canvia.
Un exemple és la il·luminació que inclou un canelobre de braços múltiples.
Una branca és un o més components connectats en sèrie. El moviment del corrent va d'un node amb una alta tensió a un node amb un valor mínim. En aquest cas, el corrent d'entrada al node coincideix amb el corrent de sortida.
Els circuits poden ser no lineals i lineals. Si en el primer hi ha un o més elements on hi ha una dependència dels valors del corrent i la tensió, en el segon les característiques dels elements no tenen aquesta dependència. A més, en circuits caracteritzats per corrent continu, la seva direcció no canvia, però en condicions de corrent altern, canvia tenint en compte el paràmetre de temps.
Característiques
El corrent altern flueix per un circuit i canvia la seva direcció amb la magnitud. Crea un camp magnètic. Per tant, sovint s'anomena corrent elèctric altern sinusoïdal periòdic. Segons la llei de la línia corba, el seu valor canvia després d'un període de temps determinat. Per això s'anomena sinusoïdal. Té la seva pròpia configuració.Dels importants, val la pena especificar el període amb freqüència, amplitud i valor instantani.
El període és el temps durant el qual es produeix un canvi de corrent elèctric i després es repeteix de nou. La freqüència és un període per segon. Es mesura en hertz, kilohertz i mil·lihertz.
Amplitud: valor màxim actual amb tensió i eficiència de flux durant un cicle complet. Valor instantani: un corrent altern o tensió que es produeix en un temps determinat.
 Especificacions de CA
Especificacions de CA
Per a AC
No obstant això, per a un circuit elèctric de CA, s'ha de tenir en compte el total, l'actiu i el reactiu, així com el factor de potència (cosF). Hem parlat de tots aquests conceptes amb més detall en aquest article.
Només observem que per trobar la potència total en una xarxa monofàsica per a corrent i tensió, cal multiplicar-los:
S=UI
El resultat s'obtindrà en volts-amperes, per tal de determinar la potència activa (watts), heu de multiplicar S pel coeficient cosФ. Es pot trobar a la documentació tècnica del dispositiu.
P=UIcos
Per determinar la potència reactiva (volts-amperes reactius), s'utilitza sinФ en comptes de cosФ.
Q=UIsin
O expressa a partir d'aquesta expressió:
I a partir d'aquí calculeu el valor desitjat.
També és fàcil trobar la potència en una xarxa trifàsica; per determinar S (total), utilitzeu la fórmula de càlcul per a la tensió actual i de fase:
S=3Uf/f
I coneixent Ulinear:
S=1,73*Uljol
1,73 o l'arrel de 3: aquest valor s'utilitza per als càlculs de circuits trifàsics.
Aleshores per analogia trobareu P actiu:
P=3Uf/f*cosФ=1,73*Uljol*cosФ
La potència reactiva es pot determinar:
Q=3Uf/f*sinФ=1,73*Uljol*sinФ
Això acaba amb la informació teòrica i passem a la pràctica.
un.Calculadora de dissipació de potència i corrent que flueix en funció de la resistència i la tensió aplicada.
Demostració en temps real de la llei d'Ohm.
Per referència
En aquest exemple, podeu augmentar la tensió i la resistència del circuit. Aquests canvis en temps real canviaran la quantitat de corrent que flueix al circuit i la potència dissipada a la resistència.
Si considerem els sistemes d'àudio, cal recordar que l'amplificador produeix una determinada tensió per a una determinada càrrega (resistència). La relació d'aquestes dues magnituds determina la potència.
L'amplificador pot emetre una quantitat limitada de tensió en funció de la font d'alimentació interna i la font de corrent. La potència que l'amplificador pot subministrar a una determinada càrrega (per exemple, 4 ohms) també està exactament limitada.
Per obtenir més potència, podeu connectar una càrrega amb una resistència menor (per exemple, 2 ohms) a l'amplificador. Tingueu en compte que quan utilitzeu una càrrega amb menys resistència, per exemple dues vegades (era 4 ohms, es va convertir en 2 ohms), la potència també es duplicarà (sempre que aquesta potència la pugui proporcionar la font d'alimentació interna i la font de corrent).
Si prenem per exemple un amplificador mono amb una potència de 100 watts en una càrrega de 4 ohms, sabent que pot lliurar una tensió de no més de 20 volts a la càrrega.
Si poseu controls lliscants a la nostra calculadora
Tensió 20 Volts
Resistència 4 ohms
Aconseguiràs
Potència 100 watts
Si moveu el control lliscant de resistència 2 ohms, veureu que la potència es duplica fins a 200 watts.
En un exemple general, la font de corrent és una bateria (no un amplificador de so), però les dependències de corrent, voltatge, resistència i resistència són les mateixes en tots els circuits.
Càlcul de circuits elèctrics
Totes les fórmules utilitzades per calcular circuits elèctrics es succeeixen.
 Relacions de característiques elèctriques
Relacions de característiques elèctriques
Així, per exemple, segons la fórmula de càlcul de potència, podeu calcular la força actual si es coneixen P i U.
Per saber quin corrent consumirà una planxa (1100 W) connectada a una xarxa de 220 V, cal que expresseu la intensitat actual a partir de la fórmula de potència:
I = P/U = 1100/220 = 5 A.
Coneixent la resistència calculada de l'espiral de l'estufa elèctrica, podeu trobar el dispositiu P. La potència a través de la resistència es troba amb la fórmula:
P = U2/R.
Hi ha diversos mètodes que permeten resoldre les tasques plantejades calculant diversos paràmetres d'un circuit determinat.
 Mètodes de càlcul de circuits elèctrics
Mètodes de càlcul de circuits elèctrics
El càlcul de potència per a circuits de diferents tipus de corrent ajuda a avaluar correctament l'estat de les línies elèctriques. Els dispositius domèstics i industrials, seleccionats d'acord amb els paràmetres donats Pnom i S, funcionaran de manera fiable i suportaran les càrregues màximes durant anys.
Com estalviar diners
La instal·lació d'un comptador de dues tarifes estalvia costos de calefacció elèctrica. Les tarifes de Moscou per a apartaments i cases equipades amb instal·lacions de calefacció elèctrica fixes distingeixen entre dos costos:
- 4.65 r de 7:00 a 23:00.
- 1.26 r de 23:00 a 7:00.
Aleshores gastareu, subjecte a funcionament les 24 hores del dia, 9 kW d'una caldera elèctrica encesa per a un terç de la potència:
9*0,3*12*4,65 + 9*0,3*12*1,26 = 150 + 40 = 190 rubles
La diferència en el consum diari és de 80 rubles. En un mes estalviareu 2400 rubles. Què justifica la instal·lació d'un comptador de dues tarifes.
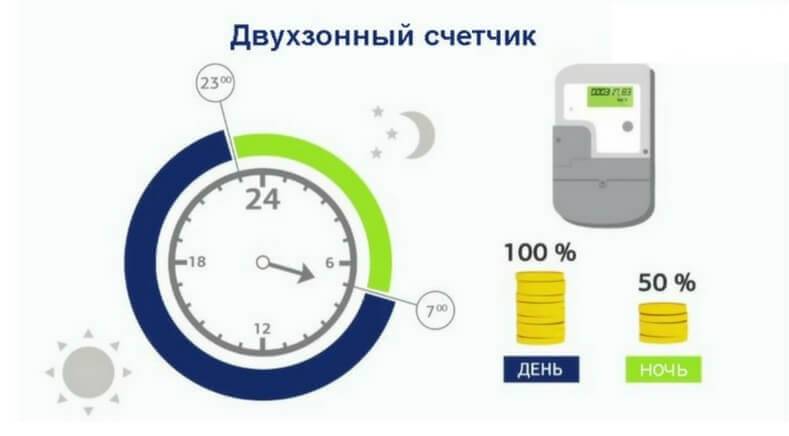
La segona manera d'estalviar diners en utilitzar un comptador de dues tarifes és utilitzar dispositius de control automàtic d'aparells elèctrics. Consisteix a assignar el pic de consum d'una caldera elèctrica, caldera i altres coses a la nit, llavors la major part de l'electricitat es carregarà a 1,26, i no a 4,65. Mentre esteu a la feina, la caldera es pot apagar completament o funcionar en mode de baixa energia, per exemple, al 10% de la potència. Per automatitzar el funcionament de la caldera elèctrica, podeu utilitzar termòstats digitals programables o calderes amb possibilitat de programar.
En conclusió, m'agradaria assenyalar que escalfar una casa amb electricitat és un mètode força car, independentment del mètode específic, ja sigui una caldera elèctrica, un convector o un altre escalfador elèctric. Només vénen a ell en els casos en què no hi ha manera de connectar-se al gas. A més dels costos de funcionament d'una caldera elèctrica, esteu esperant els costos inicials de registrar una entrada trifàsica d'electricitat.
Les tasques principals són:
- execució d'un paquet de documents, incloent especificacions tècniques, projecte elèctric, etc.;
- organització de la presa de terra;
- el cost d'un cable per connectar una casa i cablejar un cablejat nou;
- instal·lació de comptador.
A més, es pot negar una entrada trifàsica i un augment de potència si no hi ha aquesta possibilitat tècnica a la vostra zona, quan les subestacions transformadores ja funcionen al seu límit. L'elecció del tipus de caldera i calefacció depèn no només dels vostres desitjos, sinó també de les capacitats de la infraestructura.
Això conclou el nostre breu article. Esperem que ara us hagi quedat clar quin és el consum real d'electricitat d'una caldera elèctrica i com podeu reduir el cost de la calefacció d'una casa amb electricitat.
Nombre de blocs: 18 | Total de caràcters: 24761
Nombre de donants utilitzats: 7
Informació per a cada donant:
Canvi de resistència:
Al diagrama següent, podeu veure la diferència de resistència entre els sistemes representats a la part dreta i esquerra de la figura. La resistència a la pressió de l'aigua a l'aixeta és contrarestada per la vàlvula, en funció del grau d'obertura de la vàlvula, la resistència canvia.
La resistència en un conductor es mostra com un estrenyiment del conductor, com més estret és el conductor, més s'oposa al pas del corrent.
És possible que noteu que el voltatge i la pressió de l'aigua són els mateixos al costat dret i esquerre del circuit.
Cal parar atenció al fet més important. En funció de la resistència, el corrent augmenta i disminueix.
En funció de la resistència, el corrent augmenta i disminueix.
A l'esquerra, amb la vàlvula totalment oberta, veiem el major cabal d'aigua. I a la resistència més baixa, veiem el major flux d'electrons (amperatge) al conductor.
A la dreta, la vàlvula està molt més tancada i el cabal d'aigua també s'ha fet molt més gran.
L'estrenyiment del conductor també es va reduir a la meitat, la qual cosa significa que la resistència al flux de corrent s'ha duplicat. Com podem veure, pel conductor flueixen dues vegades menys electrons a causa de l'alta resistència.
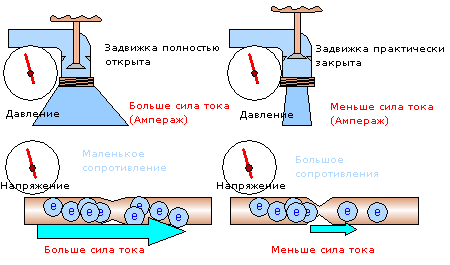
Per referència
Tingueu en compte que l'estrenyiment del conductor que es mostra al diagrama només s'utilitza com a exemple de resistència al flux de corrent. En condicions reals, l'estrenyiment del conductor no afecta molt el corrent que flueix
Els semiconductors i els dielèctrics poden proporcionar una resistència molt més gran.
El conductor cònic del diagrama es mostra només com a exemple, per entendre l'essència del procés en curs.La fórmula de la llei d'Ohm és la dependència de la resistència i la força del corrent.
I=E/R
Com podeu veure a la fórmula, la força del corrent és inversament proporcional a la resistència del circuit.
Més resistència = menys corrent
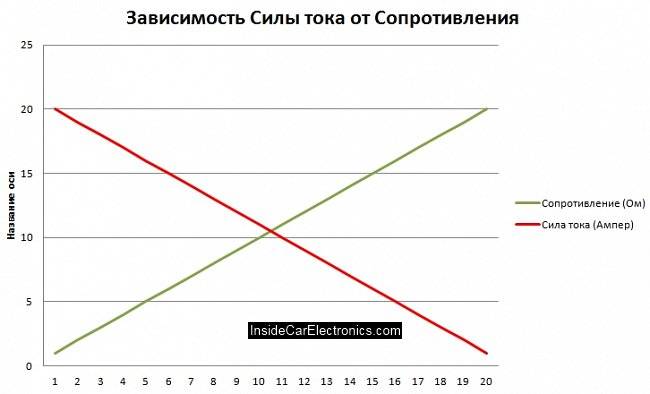
* sempre que la tensió sigui constant.
Ús de fórmules
Aquest angle caracteritza el canvi de fase en circuits U variables que contenen elements inductius i capacitius. Per calcular els components actius i reactius s'utilitzen funcions trigonomètriques, que s'utilitzen en fórmules. Abans de calcular el resultat amb aquestes fórmules, cal, mitjançant calculadores o taules de Bradis, determinar sin φ i cos φ. Després d'això, segons les fórmules
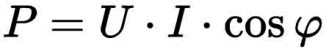
Calcularé el paràmetre desitjat del circuit elèctric. Però s'ha de tenir en compte que cadascun dels paràmetres calculats segons aquestes fórmules, a causa de la U, que canvia constantment segons les lleis de les oscil·lacions harmòniques, pot prendre un valor instantani, o un valor intermedi. . Les tres fórmules mostrades anteriorment són vàlides per a valors rms de corrent i U. Cadascun dels altres dos valors és el resultat d'un procediment de càlcul mitjançant una fórmula diferent que té en compte el pas del temps t:
Però això no són tots els matisos. Per exemple, per a les línies elèctriques, s'utilitzen fórmules que inclouen processos ondulatoris. I es veuen diferents. Però aquesta és una història completament diferent...
Per a AC
No obstant això, per a un circuit elèctric de CA, s'ha de tenir en compte el total, l'actiu i el reactiu, així com el factor de potència (cosF). Hem parlat de tots aquests conceptes amb més detall en aquest article.
Només observem que per trobar la potència total en una xarxa monofàsica per a corrent i tensió, cal multiplicar-los:
S=UI
El resultat s'obtindrà en volts-amperes, per tal de determinar la potència activa (watts), heu de multiplicar S pel coeficient cosФ. Es pot trobar a la documentació tècnica del dispositiu.
P=UIcos
Per determinar la potència reactiva (volts-amperes reactius), s'utilitza sinФ en comptes de cosФ.
Q=UIsin
O expressa a partir d'aquesta expressió:
I a partir d'aquí calculeu el valor desitjat.
També és fàcil trobar la potència en una xarxa trifàsica; per determinar S (total), utilitzeu la fórmula de càlcul per a la tensió actual i de fase:
I coneixent Ulinear:
1,73 o l'arrel de 3: aquest valor s'utilitza per als càlculs de circuits trifàsics.
Aleshores per analogia trobareu P actiu:
La potència reactiva es pot determinar:
Això acaba amb la informació teòrica i passem a la pràctica.
Preguntes sobre treball i energia elèctrica
Les preguntes teòriques per al treball i la potència del corrent elèctric poden ser les següents:
- Quina és la quantitat física de treball del corrent elèctric? (La resposta es dóna al nostre article anterior).
- Què és l'energia elèctrica? (Resposta donada més amunt).
- Definiu la llei de Joule-Lenz. Resposta: El treball d'un corrent elèctric que circula per un conductor fix amb resistència R es converteix en calor al conductor.
- Com es mesura el treball del corrent? (Resposta a dalt).
- Com es mesura la potència? (Resposta a dalt).
Aquesta és una mostra de llista de preguntes. L'essència de les qüestions teòriques en física és sempre la mateixa: comprovar la comprensió dels processos físics, la dependència d'una magnitud d'una altra, el coneixement de les fórmules i unitats de mesura adoptades en el sistema SI internacional.
Informació interessant sobre el tema
A la producció s'utilitza un esquema d'alimentació trifàsica.La tensió total d'aquesta xarxa és de 380 V. A més, aquest cablejat s'instal·la en edificis de diverses plantes i després es distribueix entre els apartaments. Però hi ha un matís que afecta la tensió final de la xarxa: connectar el nucli sota tensió resulta en 220 V. La trifàsica, a diferència de la monofàsica, no es distorsiona en connectar equips d'alimentació, ja que la càrrega es distribueix a l'escut. Però per portar una xarxa trifàsica a una casa privada, es requereix un permís especial, per tant, un esquema amb dos nuclis està molt estès, un dels quals és zero.
Normes d'alimentació de CA
El voltatge i la potència són el que tota persona que viu en un apartament o una casa particular necessita saber. La tensió de CA estàndard en un apartament i una casa privada s'expressa en una quantitat de 220 i 380 watts. Pel que fa a la determinació de la mesura quantitativa de la força de l'energia elèctrica, cal afegir el corrent elèctric a la tensió o mesurar l'indicador necessari amb un vatímetre. Al mateix temps, per fer mesures amb l'últim dispositiu, cal utilitzar sondes i programes especials.
 Què és l'alimentació CA
Què és l'alimentació CA
La potència de CA està determinada per la relació entre la quantitat de corrent i el temps, que produeix treball en un temps determinat. Un usuari normal utilitza l'indicador de potència que li transmet el proveïdor d'energia elèctrica. Com a regla general, és igual a 5-12 quilowatts. Aquestes xifres són suficients per garantir l'operativitat dels equips elèctrics domèstics necessaris.
Aquest indicador depèn de quines condicions externes per al subministrament d'energia a l'habitatge, quins dispositius limitadors de corrent (aparells automàtics o semiautomàtics) s'instal·len que regulen el moment en què els dipòsits d'energia arriben a la font del consumidor. Això es fa a diferents nivells, des del quadre elèctric domèstic fins a la unitat central de distribució elèctrica.
Normes de potència a la xarxa de CA
Mètode de conversió de circuits elèctrics
Com determinar la intensitat del corrent en circuits individuals de circuits complexos? Per resoldre problemes pràctics, no sempre cal aclarir els paràmetres elèctrics de cada element. Per simplificar els càlculs, s'utilitzen tècniques especials de conversió.
Càlcul d'un circuit amb una font d'alimentació
Per a una connexió en sèrie, s'utilitza la suma de les resistències elèctriques considerades a l'exemple:
Req = R1 + R2 + ... + Rn.
El corrent de bucle és el mateix en qualsevol punt del circuit. Podeu comprovar-ho al trencament de la secció de control amb un multímetre. Tanmateix, a cada element individual (amb diferents classificacions), el dispositiu mostrarà una tensió diferent. Per Segona llei de Kirchhoff podeu afinar el resultat del càlcul:
E = Ur1 + Ur2 + Urna.
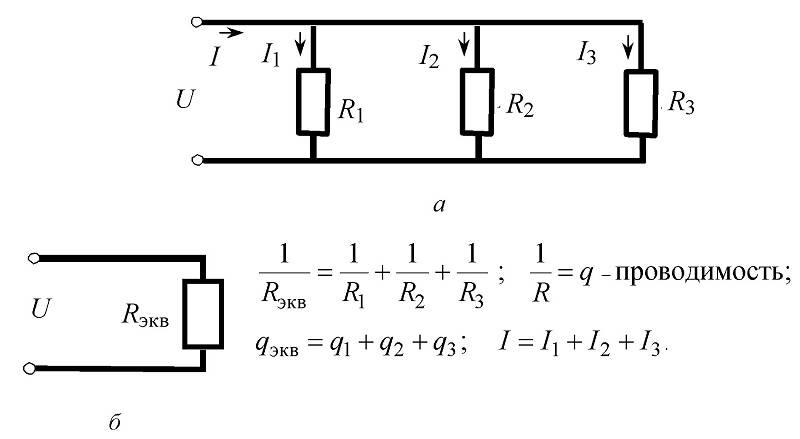 Connexió en paral·lel de resistències, circuits i fórmules per als càlculs
Connexió en paral·lel de resistències, circuits i fórmules per als càlculs
En aquesta variant, d'acord amb el primer postulat de Kirchhoff, els corrents es separen i es combinen als nodes d'entrada i sortida. La direcció que es mostra al diagrama s'escull tenint en compte la polaritat de la bateria connectada. D'acord amb els principis comentats anteriorment, es conserva la definició bàsica d'igualtat de tensió en components individuals del circuit.
L'exemple següent mostra com trobar el corrent en branques individuals. Es van prendre els següents valors inicials per al càlcul:
- R1 = 10 Ohm;
- R2 = 20 ohms;
- R3= 15 ohms;
- U = 12 V.
El següent algorisme determinarà les característiques del circuit:
fórmula bàsica per a tres elements:
Rtot = R1*R2*R3/(R1*R2 + R2*R3 + R1*R3.
- substituint les dades, calculeu Rtot = 10 * 20 * 15 / (10 * 20 + 20 * 15 + 10 * 15) = 3000 / (200 + 300 + 150) = 4,615 ohms;
- I \u003d 12 / 4,615 ≈ 2,6 A;
- I1 \u003d 12 / 10 \u003d 1,2 A;
- I2 = 12/20 = 0,6 A;
- I3 = 12/15 = 0,8 A.
Com a l'exemple anterior, es recomana comprovar el resultat del càlcul. Quan es connecten components en paral·lel, s'ha d'observar la igualtat dels corrents d'entrada i el valor total:
I \u003d 1,2 + 0,6 + 0,8 \u003d 2,6 A.
Si s'utilitza un senyal de font sinusoïdal, els càlculs es tornen més complicats. Quan un transformador està connectat a una presa de 220 V monofàsica, s'hauran de tenir en compte les pèrdues (fuites) en mode inactiu. En aquest cas, les característiques inductives dels bobinats i el coeficient d'acoblament (transformació) són essencials. La resistència elèctrica (XL) depèn dels paràmetres següents:
- freqüència del senyal (f);
- inductància (L).
Calcula XL amb la fórmula:
XL \u003d 2π * f * L.
Per trobar la resistència d'una càrrega capacitiva, l'expressió és adequada:
Xc \u003d 1 / 2π * f * C.
No s'ha d'oblidar que en circuits amb components reactius, les fases de corrent i tensió es desplacen.
Càlcul d'un circuit elèctric extens amb múltiples fonts d'alimentació
Utilitzant els principis considerats, es calculen les característiques de circuits complexos. A continuació es mostra com trobar el corrent en un circuit quan hi ha dues fonts:
- designar components i paràmetres bàsics en tots els circuits;
- feu equacions per a nodes individuals: a) I1-I2-I3=0, b) I2-I4+I5=0, c) I4-I5+I6=0;
- d'acord amb el segon postulat de Kirchhoff, es poden escriure les expressions següents per a contorns: I) E1=R1 (R01+R1)+I3*R3, II) 0=I2*R2+I4*R4+I6*R7+I3*R3 , III ) -E2=-I5*(R02+R5+R6)-I4*R4;
- comprovar: d) I3+I6-I1=0, bucle exterior E1-E2=I1*(r01+R1)+I2*R2-I5*(R02+R5+R6)+I6*R7.
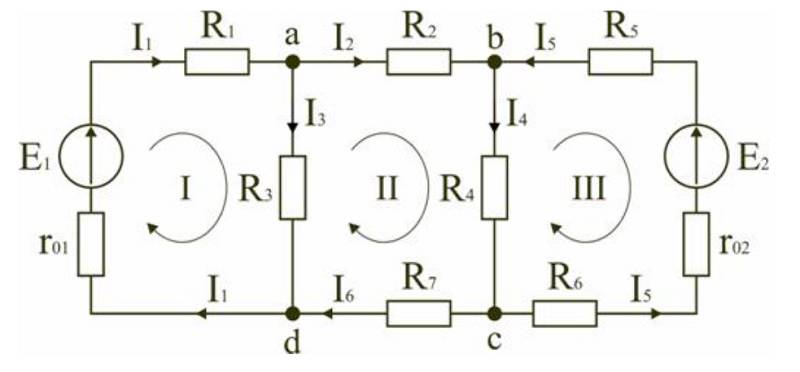 Esquema explicatiu per al càlcul amb dues fonts
Esquema explicatiu per al càlcul amb dues fonts
Càlcul de corrent per a una xarxa monofàsica
El corrent es mesura en amperes. Per calcular la potència i la tensió, s'utilitza la fórmula I = P/U, on P és la potència o càrrega elèctrica total, mesurada en watts. Aquest paràmetre s'ha d'introduir al passaport tècnic del dispositiu. U - representa la tensió de la xarxa calculada, mesurada en volts.
La relació entre corrent i tensió és clarament visible a la taula:
| Electrodomèstics i equips elèctrics | Consum d'energia (kW) | Corrent (A) |
| Rentadores | 2,0 – 2,5 | 9,0 – 11,4 |
| Cuines elèctriques estacionàries | 4,5 – 8,5 | 20,5 – 38,6 |
| microones | 0,9 – 1,3 | 4,1 – 5,9 |
| Rentaplats | 2,0 – 2,5 | 9,0 – 11,4 |
| Nevera, congelador | 0,14 – 0,3 | 0,6 – 1,4 |
| Calefacció per terra elèctrica | 0,8 – 1,4 | 3,6 – 6,4 |
| Picadora de carn elèctrica | 1,1 – 1,2 | 5,0 – 5,5 |
| Bullidor elèctric | 1,8 – 2,0 | 8,4 – 9,0 |
Així, la relació entre potència i intensitat actual permet realitzar càlculs preliminars de càrregues en una xarxa monofàsica. La taula de càlcul us ajudarà a triar la secció de cable necessària, en funció dels paràmetres.
| Diàmetres del nucli del conductor (mm) | Secció del conductor (mm2) | Conductors de coure | Conductors d'alumini | ||
| Corrent (A) | Potència, kWt) | Força (A) | Potència, kWt) | ||
| 0,8 | 0,5 | 6 | 1,3 | ||
| 0,98 | 0,75 | 10 | 2,2 | ||
| 1,13 | 1,0 | 14 | 3,1 | ||
| 1,38 | 1,5 | 15 | 3,3 | 10 | 2,2 |
| 1,6 | 2,0 | 19 | 4,2 | 14 | 3,1 |
| 1,78 | 2,5 | 21 | 4.6 | 16 | 3,5 |
| 2,26 | 4,0 | 27 | 5,9 | 21 | 4,6 |
| 2,76 | 6,0 | 34 | 7,5 | 26 | 5,7 |
| 3,57 | 10,0 | 50 | 11,0 | 38 | 8,4 |
| 4,51 | 16,0 | 80 | 17,6 | 55 | 12,1 |
| 5,64 | 25,0 | 100 | 22,0 | 65 | 14,3 |
Conclusió
Com podeu veure, trobar la potència d'un circuit o la seva secció no és gens difícil, tant si estem parlant d'una constant com d'un canvi. És més important determinar correctament la resistència total, el corrent i la tensió
Per cert, aquest coneixement ja és suficient per determinar correctament els paràmetres del circuit i seleccionar els elements: quants watts seleccionar resistències, seccions transversals de cables i transformadors. A més, aneu amb compte quan calculeu S total quan calculeu l'expressió radical.Només val la pena afegir que quan paguem factures de serveis públics, paguem per quilowatts-hora o kWh, són iguals a la quantitat d'energia consumida durant un període de temps. Per exemple, si heu connectat un escalfador de 2 quilowatts durant mitja hora, el mesurador augmentarà 1 kW / h, i durant una hora - 2 kW / h, i així successivament per analogia.
Finalment, us recomanem veure un vídeo útil sobre el tema de l'article:
Llegeix també:
- Com determinar el consum d'energia dels aparells
- Com calcular les seccions del cable
- Resistències de marcatge de potència i resistència
Resum de la lliçó
En aquesta lliçó, hem considerat diverses tasques per a la resistència mixta de conductors, així com per al càlcul de circuits elèctrics.