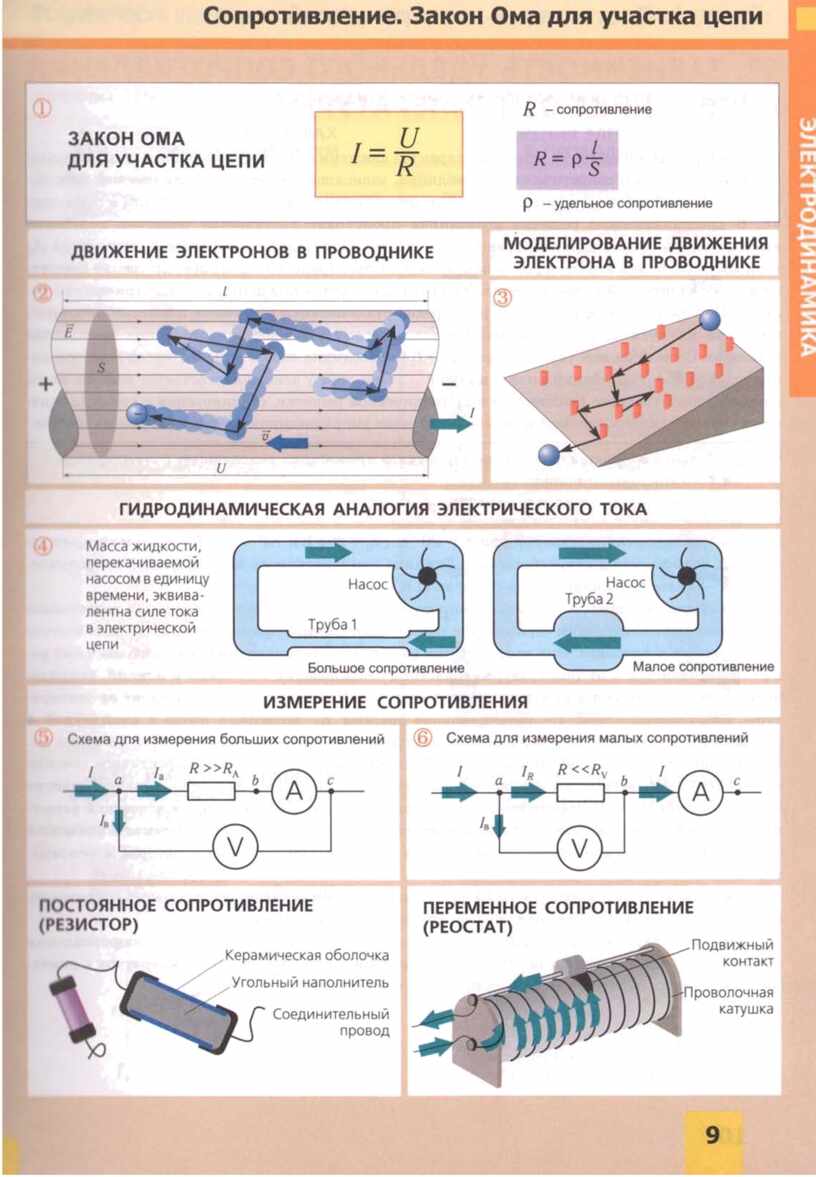
- Per a circuit tancat
- Secció separada i circuit elèctric complet
- Càlcul de la secció actual del circuit elèctric
- Opció de càlcul per a una cadena completa
- L'efecte de la llei sobre una variable
- Font EMF en un circuit complet
- R - Resistència elèctrica
- Secció no uniforme del circuit de corrent continu
- Connexió d'elements en sèrie i paral·lel
- Una cadena d'elements resistius connectats en sèrie
- Una cadena d'elements resistius connectats en paral·lel
- Formes integrals i diferencials del dret
- Entendre el corrent i la resistència
- Llei d'Ohm per al corrent altern
- Quan es produeix la llei d'Ohm
- Les lleis de Kirchhoff.
- Conceptes bàsics
- Força i tensió
- Resistència del conductor
- Interpretació de la llei d'Ohm
- Connexió en paral·lel i en sèrie
- connexió en sèrie
- Connexió paral·lel
- Què ens proporciona una connexió en paral·lel i en sèrie?
- Font ideal d'EMF
- En forma diferencial
Per a circuit tancat
Un circuit tancat significa una connexió elèctrica tancada per la qual circula el corrent. Quan hi ha una sèrie de cables connectats entre si i completant el circuit de manera que vagi d'un extrem a l'altre del cercle, serà un circuit tancat.
EMF (E): es denota i es mesura en volts i fa referència al voltatge generat per una bateria o força magnètica segons la llei de Faraday, que estableix que un camp magnètic variable en el temps induirà un corrent elèctric.
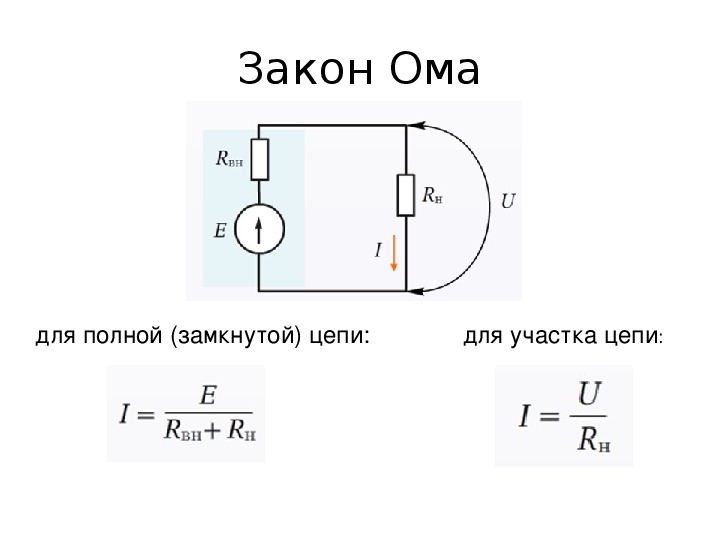
Aleshores: E = IR + Ir
E \u003d I (R + r)
I \u003d E / (R + r)
On: r és la resistència de la font de corrent.
Aquesta expressió es coneix com a llei d'Ohm dels circuits de bucle tancat.
Cadena heterogènia
Secció separada i circuit elèctric complet
La llei d'Ohm, aplicada a una secció o a tot el circuit, es pot considerar en dues opcions de càlcul:
- Secció curta separada. Forma part d'un circuit sense font EMF.
- Una cadena completa formada per una o més seccions. Això també inclou una font EMF amb la seva pròpia resistència interna.
Càlcul de la secció actual del circuit elèctric
En aquest cas, s'aplica la fórmula bàsica I \u003d U / R, en la qual I és la força del corrent, U és la tensió, R és la resistència. Segons ell, es pot formular la interpretació generalment acceptada de la llei d'Ohm:
Aquesta formulació és la base de moltes altres fórmules presentades sobre l'anomenada "camamilla" en disseny gràfic. En el sector P - es determina la potència, en els sectors I, U i R - es duen a terme accions relacionades amb la intensitat del corrent, la tensió i la resistència.
Cada expressió, tant bàsica com addicional, us permet calcular els paràmetres exactes dels elements destinats a utilitzar-se al circuit.
Els especialistes que treballen amb circuits elèctrics realitzen una determinació ràpida de qualsevol dels paràmetres mitjançant el mètode del triangle que es mostra a la figura.
Els càlculs han de tenir en compte la resistència dels conductors que connecten els elements de la secció. Com que estan fets de diferents materials, aquest paràmetre serà diferent en cada cas.Si és necessari formar un circuit complet, la fórmula principal es complementa amb els paràmetres d'una font de tensió, per exemple, una bateria.
Opció de càlcul per a una cadena completa
Un circuit complet consta de seccions individuals, combinades en un sol conjunt juntament amb una font de tensió (EMF). Així, la resistència existent de les seccions es complementa amb la resistència interna de la font connectada. Per tant, la interpretació principal comentada anteriorment serà la següent: I = U / (R + r). Aquí, l'indicador resistiu (r) de la font EMF ja s'ha afegit.
Des del punt de vista de la física pura, aquest indicador es considera un valor molt petit. Tanmateix, a la pràctica, quan es calculen circuits i circuits complexos, els especialistes es veuen obligats a tenir-ho en compte, ja que la resistència addicional afecta la precisió del treball. A més, l'estructura de cada font és molt heterogènia, com a resultat, la resistència en alguns casos es pot expressar amb taxes força altes.
Els càlculs anteriors es realitzen en relació amb circuits de corrent continu. Les accions i els càlculs amb corrent altern es fan segons un esquema diferent.
L'efecte de la llei sobre una variable
Amb el corrent altern, la resistència del circuit serà l'anomenada impedància, formada per la resistència activa i la càrrega resistiva reactiva. Això es deu a la presència d'elements amb propietats inductives i un valor de corrent sinusoïdal. La tensió també és una variable, actuant segons les seves lleis de commutació.
Per tant, un circuit de corrent altern segons la llei d'Ohm es calcula tenint en compte efectes específics: anticipar o retardar la magnitud del corrent de la tensió, així com la presència de potència activa i reactiva.Al seu torn, la reactància inclou components inductius o capacitius.
Tots aquests fenòmens correspondran a la fórmula Z \u003d U / I o Z \u003d R + J * (XL - XC), en què Z és la impedància; R - càrrega activa; XL, XC - càrregues inductives i capacitives; J és el factor de correcció.
Font EMF en un circuit complet
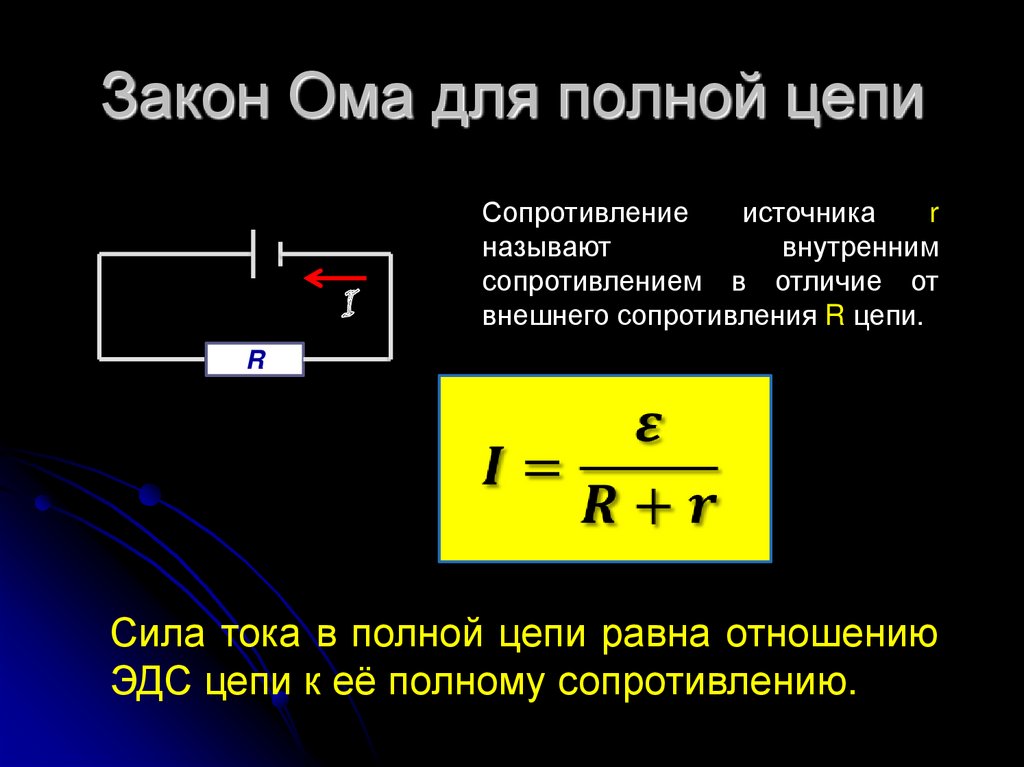
Per a l'aparició de corrent elèctric en un circuit tancat, aquest circuit ha de contenir almenys un element especial en el qual es durà a terme el treball de transferència de càrregues entre els seus pols. Les forces que porten càrregues dins d'aquest element ho fan contra el camp elèctric, la qual cosa significa que la seva naturalesa ha de ser diferent de l'elèctrica. Per tant, aquestes forces s'anomenen de tercers.
Arròs. 1. Forces externes en física.
Un element d'un circuit elèctric en el qual treballen forces externes per transferir càrregues contra l'acció d'un camp elèctric s'anomena font de corrent. La seva característica principal és la magnitud de les forces externes. Per caracteritzar-lo, s'introdueix una mesura especial - Força electromotriu (EMF), que es denota amb la lletra $\mathscr{E}$.
El valor de la FEM de la font actual és igual a la relació de forces externes per a la transferència de càrrega al valor d'aquesta càrrega:
$$\mathscr{E}={A_{st}\over q}$$
Com que el significat de la CEM és molt propera al significat de la tensió elèctrica (recordem, la tensió és la relació entre el treball realitzat pel camp elèctric que transporta la càrrega i el valor d'aquesta càrrega), aleshores la CEM, com la tensió, es mesura en Volts:
$$1B={J\overCl}$$
La segona característica elèctrica més important d'una font de corrent real és la seva resistència interna.Quan les càrregues es transfereixen entre els terminals, interaccionen amb la substància de la font EMF i, per tant, la font de corrent elèctric també presenta certa resistència. La resistència interna, com la resistència ordinària, es mesura en ohms, però es denota amb la lletra llatina minúscula $r$.

Arròs. 2. Exemples de fonts actuals.
R - Resistència elèctrica
La resistència és el recíproc del voltatge i es pot comparar amb l'efecte de moure un cos contra el moviment a l'aigua corrent. La unitat de R és Om, que es denota amb la lletra grega majúscula Omega.
El recíproc de la resistència (1/R) es coneix com a conductivitat, que mesura la capacitat d'un objecte per conduir una càrrega, expressada en unitats Siemens.
La quantitat geomètricament independent que s'utilitza s'anomena resistivitat i normalment es denota amb el símbol grec r.
Informació adicional. La llei d'Ohm ajuda a establir tres indicadors importants del funcionament de la xarxa elèctrica, que simplifica el càlcul de la potència. No és aplicable a xarxes unilaterals amb elements com ara díodes, transistors i similars. I tampoc és aplicable als elements no lineals, dels quals són exemples els tiristors, ja que el valor de la resistència d'aquests elements canvia amb diferent voltatge i corrent donats.
A freqüències més altes, el comportament distribuït esdevé dominant. El mateix passa amb les línies elèctriques molt llargues. Fins i tot a una freqüència tan baixa com 60 Hz, una línia de transmissió molt llarga, com ara 30 km, té una naturalesa distribuïda.El motiu principal és que els senyals elèctrics efectius que es propaguen en els circuits són ones electromagnètiques, no volts i amperes, que estan infectades per una ona electromagnètica. Els conductors simplement actuen com a guies de les ones. Així, per exemple, un cable coaxial mostrarà Z = 75 ohms, fins i tot si la seva resistència DC és insignificant.
La llei d'Ohm és la llei fonamental de l'enginyeria elèctrica. Té un gran nombre d'aplicacions pràctiques en tots els circuits elèctrics i components electrònics.
Els exemples més comuns d'aplicació de la llei d'Ohm:
- La potència subministrada a l'escalfador elèctric. Donada la resistència de la bobina de l'escalfador i la tensió aplicada, es pot calcular la potència subministrada a aquest escalfador.
- Elecció de fusibles. Són components de protecció que es connecten en sèrie amb dispositius electrònics. Els fusibles/CB estan classificats en amperes. El valor nominal actual del fusible es calcula mitjançant la llei d'Ohm.
- Disseny de dispositius electrònics. Els dispositius electrònics, com ara ordinadors portàtils i telèfons mòbils, requereixen una font d'alimentació de CC amb una classificació de corrent específica. Les bateries típiques dels telèfons mòbils requereixen 0,7-1 A. S'utilitza una resistència per controlar la velocitat de corrent que flueix per aquests components. La llei d'Ohm s'utilitza per calcular el corrent nominal en un circuit típic.
En un moment, les conclusions d'Ohm es van convertir en un catalitzador de noves investigacions en el camp de l'electricitat, i avui no han perdut la seva importància, ja que l'enginyeria elèctrica moderna es basa en elles. El 1841, Om va rebre el màxim honor de la Royal Society, la Medalla Copley, i el terme "Om" va ser reconegut com a unitat de resistència ja el 1872.
Secció no uniforme del circuit de corrent continu
Una estructura heterogènia té una secció del circuit, on, a més de conductors i elements, hi ha una font de corrent. El seu EMF s'ha de tenir en compte a l'hora de calcular la intensitat total del corrent en aquesta zona.
Hi ha una fórmula que defineix els principals paràmetres i processos d'un lloc heterogeni: q = q0 x n x V. Els seus indicadors es caracteritzen de la següent manera:
- En el procés de moviment de càrregues (q), adquireixen una certa densitat. El seu rendiment depèn de la força actual i de l'àrea de la secció transversal del conductor (S).
- En condicions d'una determinada concentració (n), és possible indicar amb precisió el nombre de càrregues unitàries (q0) que es van moure en un sol període de temps.
- Per als càlculs, el conductor es considera condicionalment una secció cilíndrica amb algun volum (V).
En connectar el conductor a la bateria, aquesta es descarregarà al cap d'un temps. És a dir, el moviment dels electrons s'alenteix gradualment i, al final, s'atura del tot. Això es veu facilitat per la xarxa molecular del conductor, que contraresta la col·lisió d'electrons entre si i amb altres factors. Per superar aquesta resistència, s'han d'aplicar, a més, determinades forces de tercers.
Durant els càlculs, aquestes forces s'afegeixen a les de Coulomb. A més, per transferir un càrrec unitari q del 1r punt al 2n, caldrà realitzar el treball A1-2 o simplement A12. Amb aquesta finalitat, es crea una diferència de potencial (ϕ1 - ϕ2). Sota l'acció d'una font de corrent continu, sorgeix un EMF, movent càrregues al llarg del circuit. La magnitud de la tensió total constarà de totes les forces esmentades anteriorment.
En els càlculs s'ha de tenir en compte la polaritat de la connexió a l'alimentació de CC. Quan es canvien els terminals, també canviarà l'EMF, accelerant o alentint el moviment de les càrregues.
Connexió d'elements en sèrie i paral·lel
Per als elements d'un circuit elèctric (secció d'un circuit), un moment característic és una connexió en sèrie o paral·lel.
En conseqüència, cada tipus de connexió s'acompanya d'una naturalesa diferent del flux de corrent i el subministrament de tensió. En aquest sentit, la llei d'Ohm també s'aplica de diferents maneres, segons l'opció d'incloure elements.
Una cadena d'elements resistius connectats en sèrie
Pel que fa a una connexió en sèrie (secció d'un circuit amb dos components), s'utilitza la redacció:
- jo = jo1 = jo2 ;
- U = U1 + U2 ;
- R=R1 + R2
Aquesta formulació demostra clarament que, independentment del nombre de components resistius connectats en sèrie, el corrent que flueix en una secció del circuit no canvia de valor.
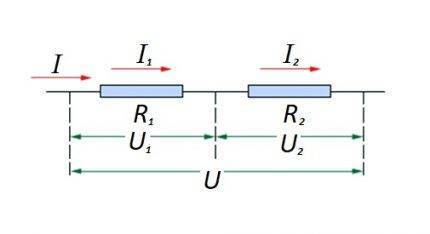 Connexió d'elements resistius en una secció de circuit en sèrie entre si. Aquesta opció té la seva pròpia llei de càlcul. Al diagrama: I, I1, I2 - flux de corrent; R1, R2 - elements resistius; U, U1, U2 - tensió aplicada
Connexió d'elements resistius en una secció de circuit en sèrie entre si. Aquesta opció té la seva pròpia llei de càlcul. Al diagrama: I, I1, I2 - flux de corrent; R1, R2 - elements resistius; U, U1, U2 - tensió aplicada
La quantitat de tensió aplicada als components resistius actius del circuit és la suma i suma el valor de la font EMF.
En aquest cas, la tensió de cada component individual és: Ux = I * Rx.
La resistència total s'ha de considerar com la suma dels valors de tots els components resistius del circuit.
Una cadena d'elements resistius connectats en paral·lel
En el cas que hi hagi una connexió paral·lela de components resistius, la formulació es considera justa respecte a la llei del físic alemany Ohm:
- jo = jo1 + jo2 … ;
- U = U1 = U2 … ;
- 1/R = 1/R1 + 1/R2 + …
Les opcions per compilar seccions de circuit de tipus "mixt" no s'exclouen quan s'utilitzen connexions en paral·lel i en sèrie.
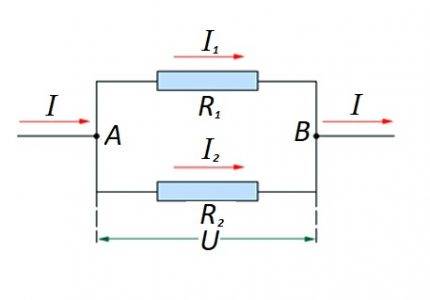 La connexió d'elements resistius en una secció de circuit en paral·lel entre si. Per a aquesta opció s'aplica la seva pròpia llei de càlcul. Al diagrama: I, I1, I2 - flux de corrent; R1, R2 - elements resistius; U - tensió aplicada; A, B - punts d'entrada / sortida
La connexió d'elements resistius en una secció de circuit en paral·lel entre si. Per a aquesta opció s'aplica la seva pròpia llei de càlcul. Al diagrama: I, I1, I2 - flux de corrent; R1, R2 - elements resistius; U - tensió aplicada; A, B - punts d'entrada / sortida
Per a aquestes opcions, el càlcul es realitza normalment mitjançant el càlcul inicial de la qualificació resistiva de la connexió paral·lela. Aleshores s'afegeix al resultat el valor de la resistència connectada en sèrie.
Formes integrals i diferencials del dret
Tots els punts anteriors amb càlculs són aplicables a les condicions en què els conductors d'una estructura "homogènia", per dir-ho així, s'utilitzen com a part dels circuits elèctrics.
Mentrestant, a la pràctica, sovint s'ha de fer front a la construcció d'un esquema, on l'estructura dels conductors canvia en diferents zones. Per exemple, s'utilitzen cables de secció transversal més gran o, per contra, més petits, fets a partir de diferents materials.
Per tenir en compte aquestes diferències, hi ha una variació de l'anomenada "llei d'Ohm diferencial-integral". Per a un conductor infinitament petit, el nivell de densitat de corrent es calcula en funció de la intensitat i del valor de conductivitat.
Sota el càlcul diferencial, es pren la fórmula: J = ό * E
Per al càlcul integral, respectivament, la formulació: I * R = φ1 - φ2 + έ
Tanmateix, aquests exemples s'acosten més a l'escola de matemàtiques superiors i en realitat no s'utilitzen en la pràctica real d'un simple electricista.
Entendre el corrent i la resistència
Comencem pel concepte de corrent elèctric.En resum, el corrent elèctric en relació amb els metalls és el moviment dirigit dels electrons: partícules carregades negativament. Normalment es representen com petits cercles. En un estat de calma, es mouen de manera caòtica, canviant constantment de direcció. En determinades condicions, l'aparició d'una diferència de potencial, aquestes partícules comencen un cert moviment en alguna direcció. Aquest moviment és el corrent elèctric.
Per fer-ho més clar, podem comparar electrons amb aigua vessada en algun pla. Mentre l'avió estigui estacionari, l'aigua no es mou. Però, tan bon punt va aparèixer un pendent (va sorgir una diferència de potencial), l'aigua va començar a moure's. Passa el mateix amb els electrons.
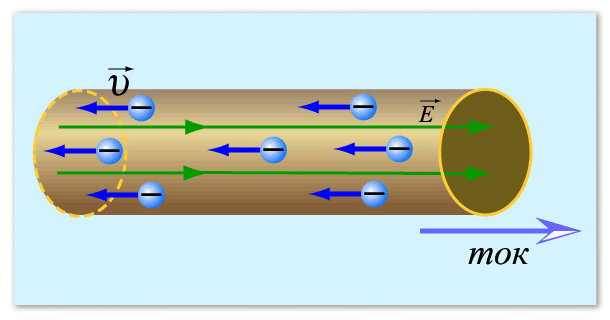
Així és com es pot imaginar un corrent elèctric
Ara hem d'entendre què és la resistència i per què tenen retroalimentació amb la força del corrent: com més gran sigui la resistència, menor serà el corrent. Com sabeu, els electrons es mouen a través d'un conductor. Normalment es tracta de cables metàl·lics, ja que els metalls tenen una bona capacitat de conduir l'electricitat. Sabem que el metall té una densa xarxa cristal·lina: moltes partícules properes i interconnectades. Els electrons, fent camí entre els àtoms metàl·lics, xoquen amb ells, cosa que els dificulta el moviment. Això ajuda a il·lustrar la resistència que exerceix un conductor. Ara queda clar per què com més gran és la resistència, menor és la intensitat del corrent: com més partícules, més difícil és que els electrons superin el camí, ho fan més lentament. Això sembla que s'ha resolt.
Si voleu provar aquesta dependència empíricament, trobeu una resistència variable, connecteu en sèrie una resistència, un amperímetre, una font de corrent (bateria).També és desitjable inserir un interruptor al circuit: un interruptor de palanca normal.
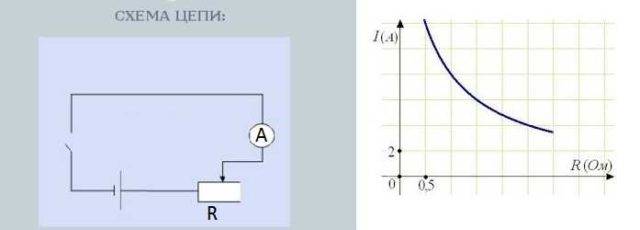
Circuit per provar la dependència del corrent de la resistència
Girar el botó de la resistència canvia la resistència. Al mateix temps, també canvien les lectures de l'amperímetre, que mesura la força actual. A més, com més gran sigui la resistència, menys es desvia la fletxa, menys corrent. Com més baixa sigui la resistència, més forta es desvia la fletxa: el corrent és més gran.
La dependència del corrent de la resistència és gairebé lineal, és a dir, es reflecteix al gràfic com una línia gairebé recta. Per què gairebé? Això s'hauria de parlar per separat, però això és una altra història.
Llei d'Ohm per al corrent altern
Quan es calculen circuits de CA, en comptes del concepte de resistència, s'introdueix el concepte d'"impedància". La impedància es denota amb la lletra Z, inclou la resistència activa de la càrrega Ra i la reactància X (o Rr). Això es deu a la forma del corrent sinusoïdal (i als corrents de qualsevol altra forma) i als paràmetres dels elements inductius, així com a les lleis de commutació:
- El corrent en un circuit inductiu no pot canviar a l'instant.
- La tensió en un circuit amb una capacitat no pot canviar a l'instant.
Així, el corrent comença a retardar o conduir la tensió, i la potència aparent es divideix en activa i reactiva.
U=I/Z
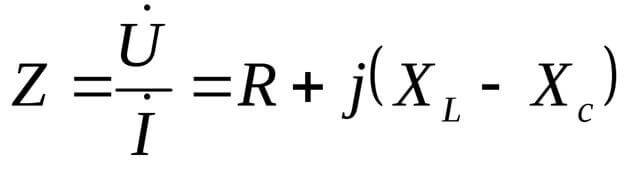
XL i XC són els components reactius de la càrrega.
En aquest sentit, s'introdueix el valor cosФ:
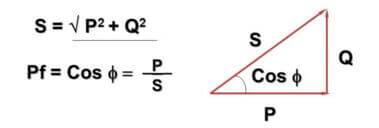
Aquí - Q - potència reactiva a causa del corrent altern i components inductius-capacitius, P - potència activa (dissipada en components actius), S - potència aparent, cosФ - factor de potència.
Potser heu notat que la fórmula i la seva representació es creuen amb el teorema de Pitàgores. Això és cert i l'angle Ф depèn de la mida del component reactiu de la càrrega: com més gran és, més gran és.A la pràctica, això porta al fet que el corrent que flueix realment a la xarxa és més gran que el que té en compte un comptador domèstic, mentre que les empreses paguen per tota la potència.
En aquest cas, la resistència es presenta en forma complexa:
Aquí j és una unitat imaginària, que és típica per a la forma complexa d'equacions. Menys conegut com i, però en enginyeria elèctrica, també es denota el valor efectiu del corrent altern, per tant, per no confondre's, és millor utilitzar j.
La unitat imaginària és √-1. És lògic que no hi hagi aquest nombre quan es quadra, la qual cosa pot donar lloc a un resultat negatiu de "-1".
Quan es produeix la llei d'Ohm
Crear condicions ideals no és fàcil. Fins i tot en conductors purs, la resistència elèctrica varia amb la temperatura. La seva disminució minimitza l'activitat de les molècules de la xarxa cristal·lina, la qual cosa simplifica el moviment de les càrregues lliures. A un cert nivell de "congelació" es produeix l'efecte de la superconductivitat. L'efecte contrari (deteriorament de la conductivitat) s'observa quan s'escalfa.
Al mateix temps, els electròlits, metalls i certs tipus de ceràmiques conserven la resistència elèctrica independentment de la densitat de corrent. L'estabilitat dels paràmetres mantenint un determinat règim de temperatura permet aplicar les fórmules de la llei d'Ohm sense correccions addicionals.
Els materials i gasos semiconductors es caracteritzen per una resistència elèctrica variable. Aquest paràmetre es veu afectat significativament per la intensitat de corrent en el volum de control. Per calcular les característiques de rendiment s'han d'aplicar mètodes de càlcul especialitzats.
Si es considera corrent altern, es corregeix el mètode de càlcul.En aquest cas, s'haurà de tenir en compte la presència de components reactius. Amb la naturalesa resistiva de la resistència, és possible aplicar les tecnologies de càlcul considerades basades en les fórmules de la llei d'Ohm.
Les lleis de Kirchhoff.
Distribució
corrents a les branques del circuit elèctric
obeeix la primera llei de Kirchhoff,
i la distribució de tensions en seccions
cadena obeeix la segona llei de Kirchhoff.
Les lleis de Kirchhoff
juntament amb la llei d'Ohm són les principals
en la teoria dels circuits elèctrics.
El primer
Llei de Kirchhoff:
Algebraica
la suma dels corrents del node és zero:
i
= 0 (19)
On
i
és el nombre de branques que convergeixen en un node donat.
És a dir, suma
s'estén als corrents de les branques,
que convergeixen en el considerat
node.
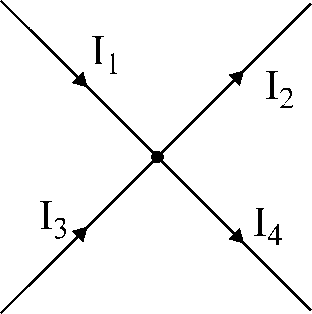
Fig.17. Il·lustració
a la primera llei de Kirchhoff.
Número
equacions compilades segons la primera
La llei de Kirchhoff està determinada per la fórmula:
Nup
= Núm
– 1,
On
Nu
és el nombre de nodes de la cadena considerada.
Senyals de corrents d'entrada
les equacions es prenen tenint en compte les escollides
direcció positiva. Senyals a
els corrents són els mateixos si els corrents són els mateixos
orientat en relació a això
node.
Per exemple,
per al node que es mostra a la figura 17:
assignem signes als corrents que flueixen al node
"+", i als corrents que flueixen des del node - signes
«-».
Després l'equació
segons la primera llei de Kirchhoff, s'escriurà
Tan:
jo1
– I2
+ jo3
– I4
= 0.
equacions,
compilat segons la primera llei de Kirchhoff,
s'anomenen nodes.
Això
la llei expressa el fet que en el node
la càrrega elèctrica no s'acumula
i no es consumeix. La quantitat d'electricitat
els càrrecs que arriben al lloc són iguals a la suma
càrregues que surten del node en un mateix
mateix període de temps.
Segon
Llei de Kirchhoff:
Algebraica
suma de fem en qualsevol circuit tancat
cadena és igual a la suma algebraica de les caigudes
tensió als elements d'aquest circuit:
Ui
=
Ei
IiRi=Ei(20)
On
i
- número d'element (resistència o
font de tensió) en la considerada
contorn.
**Número
equacions compilades segons la segona
La llei de Kirchhoff està determinada per la fórmula:
Nup
= Nb
- Nu
+ 1 – Ned.s.
On
Nb
- el nombre de branques del circuit elèctric;
Nu
— nombre de nodes;
Ned.s.
és el nombre de fonts de fem ideals.
Fig.18. Il·lustració
a la segona llei de Kirchhoff.
Per,
escriure correctament la segona llei
Kirchhoff per a un contorn determinat, segueix
complir amb les normes següents:
-
arbitràriament
seleccioneu la direcció de la derivació del contorn,
per exemple, en sentit horari (Fig. 18). -
emf
i caigudes de tensió que coincideixen
en la direcció amb la direcció seleccionada
bypass s'escriuen en una expressió amb
signe "+"; si e.f.s. i caiguda de tensió
no coincideix amb la direcció
contorn, després van precedits d'un signe
«-».
Per exemple,
per al contorn de la figura 18, segona llei de Kirchhoff
s'escriurà de la següent manera:
U1
–U2
+ U3
= E1
–E3
–E4
(21)
L'equació (20) pot ser
reescriure com:
(Ui
– Ei)
= 0 (22)
On
(U
– E)
- tensió a la branca.
Conseqüentment,
Es pot formular la segona llei de Kirchhoff
de la següent manera:
Algebraica
la suma de les tensions a les branques en qualsevol
bucle tancat és zero.
Potencial
serveix el diagrama comentat anteriorment
interpretació gràfica del segon
la llei de Kirchhoff.
Tasca número 1.
AT
el circuit de la figura 1 rep corrents I1
i jo3,
resistència i fem Determinar corrents
jo4,
jo5,
jo6
; tensió entre punts a
i b
si jo1
= 10 mA,
jo3
= -20 mA,
R4
= 5 kOhm,
E5
= 20B,
R5
= 3kOhm,
E6
= 40B,
R6
= 2 kOhm.
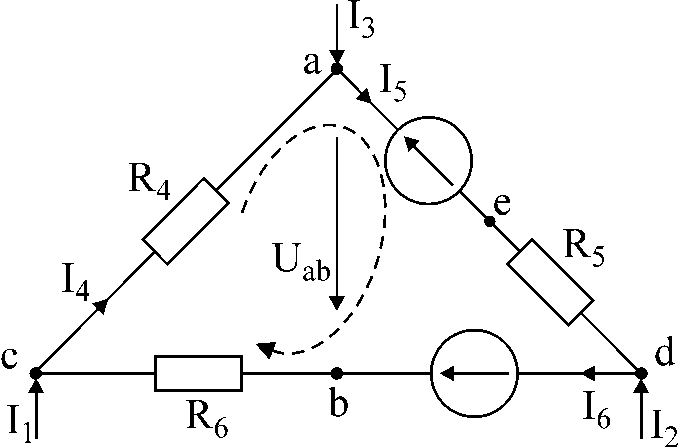
Fig.1
Solució:
-
Per un donat
contorn, componem dues equacions segons
La primera llei de Kirchhoff i una - segons
segon. Direcció del contorn
indicat per una fletxa.

AT
com a resultat de la solució obtenim: I6
= 0; jo4
= 10 mA;
jo5
= -10 mA
-
preguntar
direcció de tensió entre punts
a
i b
des del punt "a"
a punt "b"
—Uab.
Aquesta tensió es pot trobar a partir de l'equació
Segona llei de Kirchhoff:
jo4R4
+ Uab
+ jo6R6
= 0
Uab
= - 50 V.
Tasca número 2.
Per
els diagrames de la figura 2 elaboren equacions segons
Les lleis de Kirchhoff i determinen les incògnites
punts.
Donat:
jo1
= 20 mA;
jo2
= 10 mA
R1
= 5 kOhm,
R3
= 4kOhm,
R4
= 6kOhm,
R5
= 2 kOhm,
R6
= 4kΩ.
Fig.2
Solució:
Nombre de nodes
equacions - 3, el nombre d'equacions de contorn
– 1.
Recordeu!
En compilar l'equació segons la segona
Llei de Kirchhoff, triem el contorn, en
que no inclou les fonts actuals.
La direcció del contorn s'indica a la figura.
AT
d'aquest circuit, els corrents de les branques I1
i jo2.
Desconegut
corrents
jo3,
jo4,
jo5,
jo6.

Decidir
sistema, obtenim: I3
= 13,75 mA;
jo4
= -3,75 mA;
jo5
= 6,25 mA;
jo6
= 16,25 mA.
Conceptes bàsics
El corrent elèctric flueix quan un circuit tancat permet que els electrons es moguin d'un potencial alt a un de més baix del circuit. És a dir, el corrent requereix una font d'electrons que tingui l'energia per posar-los en moviment, així com un punt de retorn de les càrregues negatives, que es caracteritza per la seva deficiència. Com a fenomen físic, el corrent en un circuit es caracteritza per tres magnituds fonamentals:
- voltatge;
- força actual;
- la resistència d'un conductor per on es mouen els electrons.
Força i tensió
La intensitat del corrent (I, mesurada en amperes) és el volum d'electrons (càrrega) que es mouen per un lloc del circuit per unitat de temps.En altres paraules, la mesura I és la determinació del nombre d'electrons en moviment
És important entendre que el terme només es refereix al moviment: les càrregues estàtiques, per exemple, als terminals d'una bateria no connectada, no tenen un valor mesurable de I. El corrent que flueix en una direcció s'anomena directa (DC) i el canvi de direcció periòdicament s'anomena alterna (AC). El voltatge es pot il·lustrar amb un fenomen com la pressió o com la diferència en l'energia potencial dels objectes sota la influència de la gravetat.
Per tal de crear aquest desequilibri, primer heu de gastar energia, que es realitzarà en moviment en les circumstàncies adequades. Per exemple, en la caiguda d'una càrrega des d'una alçada, es treballa per aixecar-la, a les bateries galvàniques, la diferència de potencial als terminals es forma a causa de la conversió d'energia química, en generadors, com a resultat de l'exposició a un camp electromagnètic
L'estrès es pot il·lustrar per un fenomen com la pressió, o com la diferència en l'energia potencial dels objectes sota la influència de la gravetat. Per tal de crear aquest desequilibri, primer heu de gastar energia, que es realitzarà en moviment en les circumstàncies adequades. Per exemple, en la caiguda d'una càrrega des d'una alçada, es realitza el treball d'aixecar-la, a les bateries galvàniques la diferència de potencial als terminals es forma a causa de la conversió d'energia química, en generadors, com a resultat de l'exposició a un camp electromagnètic.
Resistència del conductor
Per molt que sigui un conductor normal, mai permetrà que els electrons passin sense una certa resistència al seu moviment.És possible considerar la resistència com un anàleg de la fricció mecànica, encara que aquesta comparació no serà perfecta. Quan el corrent flueix per un conductor, una mica de diferència de potencial es converteix en calor, de manera que sempre hi haurà una caiguda de tensió a través de la resistència. Els escalfadors elèctrics, assecadors de cabells i altres dispositius similars estan dissenyats únicament per dissipar l'energia elèctrica en forma de calor.
La resistència simplificada (indicada com R) és una mesura de quant es retarda el flux d'electrons en un circuit. Es mesura en ohms. La conductivitat d'una resistència o d'un altre element està determinada per dues propietats:
- geometria;
- material.
La forma és de la màxima importància, com es desprèn de l'analogia hidràulica: empènyer l'aigua per una canonada llarga i estreta és molt més difícil que empènyer l'aigua per una de curta i ampla. Els materials juguen un paper decisiu. Per exemple, els electrons es poden moure lliurement en un fil de coure, però no poden fluir en absolut a través d'aïllants com el cautxú, independentment de la seva forma. A més de la geometria i el material, hi ha altres factors que afecten la conductivitat.
Interpretació de la llei d'Ohm
Per garantir el moviment de les càrregues, cal tancar el circuit. En absència de potència addicional, el corrent no pot existir durant molt de temps. Els potencials es tornaran ràpidament iguals. Per mantenir el mode de funcionament del circuit, es necessita una font addicional (generador, bateria).
El circuit complet contindrà la resistència elèctrica total de tots els components. Per a càlculs precisos, es tenen en compte les pèrdues en conductors, elements resistius i una font d'alimentació.
La quantitat de tensió que s'ha d'aplicar per a una determinada intensitat de corrent es calcula mitjançant la fórmula:
U=I*R.
De la mateixa manera, amb l'ajuda de les relacions considerades, es determinen altres paràmetres del circuit.
Connexió en paral·lel i en sèrie
En electricitat, els elements es connecten en sèrie, un darrere l'altre o en paral·lel, és quan es connecten diverses entrades a un punt i les sortides dels mateixos elements es connecten a un altre.
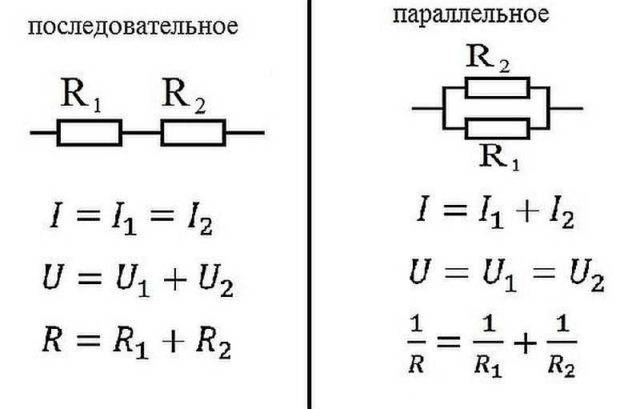
Llei d'Ohm per a la connexió en paral·lel i en sèrie
connexió en sèrie
Com funciona la llei d'Ohm en aquests casos? Quan es connecta en sèrie, el corrent que flueix per la cadena d'elements serà el mateix. La tensió d'una secció d'un circuit amb elements connectats en sèrie es calcula com la suma de les tensions de cada secció. Com es pot explicar això? El flux de corrent a través d'un element és la transferència d'una part de la càrrega d'una part a una altra. Vull dir, és una mica de feina. La magnitud d'aquest treball és la tensió. Aquest és el significat físic de l'estrès. Si això està clar, seguim endavant.
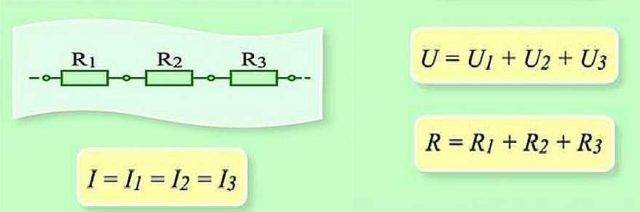
Connexió sèrie i paràmetres d'aquest tram del circuit
Quan es connecta en sèrie, cal transferir la càrrega al seu torn a través de cada element. I sobre cada element, aquest és un cert "volum" de treball. I per trobar la quantitat de treball a tota la secció de la cadena, cal afegir el treball a cada element. Així doncs, resulta que la tensió total és la suma de les tensions de cadascun dels elements.
De la mateixa manera, amb l'ajuda de l'addició, també es troba la resistència total de la secció del circuit. Com t'ho pots imaginar? El corrent que circula per la cadena d'elements supera seqüencialment totes les resistències. Un per un. És a dir, per trobar la resistència que va vèncer, cal sumar les resistències. Més o menys així.La derivació matemàtica és més complicada, i és més fàcil entendre el mecanisme d'aquesta llei.
Connexió paral·lel
Una connexió paral·lela és quan els inicis dels conductors/elements convergeixen en un punt, i en un altre els seus extrems estan connectats. Intentarem explicar les lleis vàlides per a compostos d'aquest tipus. Comencem pel corrent. Un corrent d'alguna magnitud es subministra al punt de connexió dels elements. Se separa, travessant tots els conductors. D'això concloem que la intensitat total de la secció és igual a la suma de la intensitat de cadascun dels elements: I = I1 + I2 + I3.
Ara pel voltatge. Si el voltatge és treball per moure una càrrega, aleshores el treball que es necessita per moure una càrrega serà el mateix en qualsevol element. És a dir, la tensió de cada element connectat en paral·lel serà la mateixa. U=U1=U2=U3. No tan divertit i visual com en el cas de l'explicació de la llei d'Ohm per a una secció de cadena, però ho podeu entendre.
Lleis per a la connexió paral·lela
Per a la resistència, les coses són una mica més complicades. Introduïm el concepte de conductivitat. Aquesta és una característica que indica com de fàcil o difícil és que una càrrega passi per aquest conductor. És evident que com més baixa sigui la resistència, més fàcil serà que passi el corrent. Per tant, la conductivitat - G - es calcula com el recíproc de la resistència. A la fórmula, es veu així: G = 1/R.
Per què parlem de conductivitat? Perquè la conductivitat total d'una secció amb una connexió paral·lela d'elements és igual a la suma de la conductivitat de cadascuna de les seccions. G = G1 + G2 + G3 - fàcil d'entendre. La facilitat amb què el corrent superarà aquest node d'elements paral·lels depèn de la conductivitat de cadascun dels elements. Així que resulta que s'han de plegar.
Ara podem passar a la resistència.Com que la conductivitat és el recíproc de la resistència, podem obtenir la fórmula següent: 1/R = 1/R1 + 1/R2 + 1/R3.
Què ens proporciona una connexió en paral·lel i en sèrie?
Els coneixements teòrics són bons, però com aplicar-los a la pràctica? Els elements de qualsevol tipus es poden connectar en paral·lel i en sèrie. Però només vam considerar les fórmules més simples que descriuen elements lineals. Els elements lineals són resistències, que també s'anomenen "resistències". Així que aquí teniu com podeu utilitzar el que heu après:
Si no hi ha resistències de gran valor disponible, però n'hi ha diverses de més petites, la resistència desitjada es pot obtenir connectant diverses resistències en sèrie. Com podeu veure, aquesta és una tècnica útil.
Per allargar la vida útil de les bateries, es poden connectar en paral·lel. La tensió en aquest cas, segons la llei d'Ohm, continuarà sent la mateixa (pot assegurar-se mesurant la tensió amb un multímetre). I la "vida útil" d'una bateria dual serà molt més llarga que la de dos elements que es substituiran mútuament
Tingueu en compte que només es poden connectar en paral·lel fonts d'alimentació amb el mateix potencial. És a dir, no es pot connectar una bateria morta i una nova.
Si encara us connecteu, la bateria que té una càrrega més gran tendirà a carregar-ne una de menys carregada. Com a resultat, la seva càrrega total baixarà a un valor baix.
En general, aquests són els usos més habituals d'aquests compostos.
Font ideal d'EMF
La força electromotriu (E) és una magnitud física que determina el grau d'influència de les forces externes sobre el moviment en un circuit tancat de portadors de càrrega. En altres paraules, amb quina força tendeix a fluir el corrent a través del conductor dependrà de l'EMF.
Quan expliquen fenòmens tan incomprensibles, als mestres domèstics els agrada recórrer al mètode de les analogies hidràuliques. Si un conductor és una canonada i el corrent elèctric és la quantitat d'aigua que hi flueix, aleshores l'EMF és la pressió que desenvolupa una bomba per bombejar fluid.
El terme força electromotriu està relacionat amb un concepte com el voltatge. Ella, EMF, també es mesura en volts (unitat - "V"). Cada font d'energia, ja sigui una bateria, un generador o un panell solar, té la seva pròpia força electromotriu. Sovint, aquest EMF s'acosta a la tensió de sortida (U), però sempre una mica inferior. Això és causat per la resistència interna de la font, sobre la qual una part de la tensió cau inevitablement.
Per aquest motiu, la font ideal de CEM és més aviat un concepte abstracte o un model físic que no té cabuda en el món real, perquè la resistència interna de la bateria Rin, encara que molt baixa, encara és diferent del zero absolut.
Font ideal i real de fem
En forma diferencial
La fórmula es presenta molt sovint en forma diferencial, ja que el conductor sol ser no homogeni i caldrà trencar-lo en les seccions més petites possibles. El corrent que la travessa està associat a la magnitud i la direcció, per la qual cosa es considera una magnitud escalar. Sempre que s'ha de trobar el corrent resultant a través d'un cable, es pren la suma algebraica de tots els corrents individuals. Com que aquesta regla només s'aplica a les magnituds escalars, el corrent també es pren com una quantitat escalar. Se sap que el corrent dI = jdS passa per la secció. La tensió és igual a Edl, aleshores per a un cable amb una secció transversal constant i la mateixa longitud, la relació serà certa:
 Forma diferencial
Forma diferencial
Per tant, l'expressió del corrent en forma vectorial serà: j = E.
Important! En el cas dels conductors metàl·lics, la conductivitat disminueix amb l'augment de la temperatura, mentre que per als semiconductors augmenta. La llei d'Omov no demostra una estricta proporcionalitat
La resistència d'un gran grup de metalls i aliatges desapareix a una temperatura propera al zero absolut, i el procés s'anomena superconductivitat.